一人暮らしのエンゲル係数・食費の目安は？上手な貯蓄術と合わせて解説！

エンゲル係数とは家計の消費支出に占める食料費の割合です。
食料費は生活する上で最も必要な品目のため、一般に数値が下がると生活水準が上がり、逆に数値が上がると生活水準が下がる目安とされています。

ここ数年、エンゲル係数は上昇が続いていますが、一人暮らしのエンゲル係数はどのくらいでしょうか。

一人暮らしのエンゲル係数について統計を基に実態を明らかにし、賢い節約方法や貯蓄術もあわせて解説します。

• エンゲル係数とは
• 上昇するエンゲル係数
• 一人暮らしのエンゲル係数
• 食料費の節約法と貯蓄術
• おわりに

エンゲル係数とは

エンゲル係数とは、消費支出に占める食料費の割合で、以下のように求められます。*1

　　エンゲル係数 = 食料費 ÷ 消費支出 × 100

一般的に、所得が低いほど生活に必要な食料費の割合が大きくなるためエンゲル係数は高くなり、一方、所得が高いほど低くなる傾向にあります。
これを「エンゲルの法則」と呼びます。*2

ただし、収入がある額以下になると、固定的な支出に圧迫されて食料費が削られるため、収入が低いにもかかわらずエンゲル係数は小さくなるというエンゲル法則の逆転現象も生じます。*3

上昇するエンゲル係数

日本国内のエンゲル係数は所得水準の向上により長期にわたって低下しましたが、2000 年代に入って下げ止まり、2020年以降は大幅に上昇しています。*2

二人以上世帯のエンゲル係数の上昇

二人以上世帯のエンゲル係数は2023年に26.5％まで上昇し、2024年にはさらに27.1％まで上がっています（図1）。*4

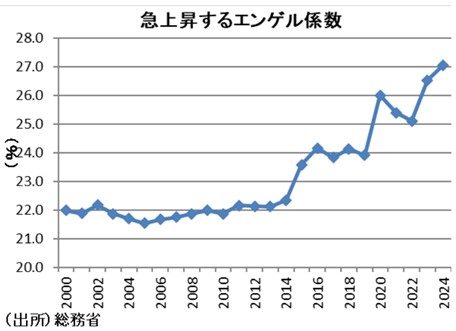
図1　急上昇するエンゲル係数

エンゲル係数上昇の原因

エンゲル係数上昇の原因はなんでしょうか。
エコノミストは食料品価格の上昇が原因であると分析しています。*2
国際的な食料品価格の上昇や円安の進行などの影響で、食料品価格の上昇は物価全体の伸びを大きく上回っています。

以下の図2は2012年以降の物価指数の推移を表しています。*5

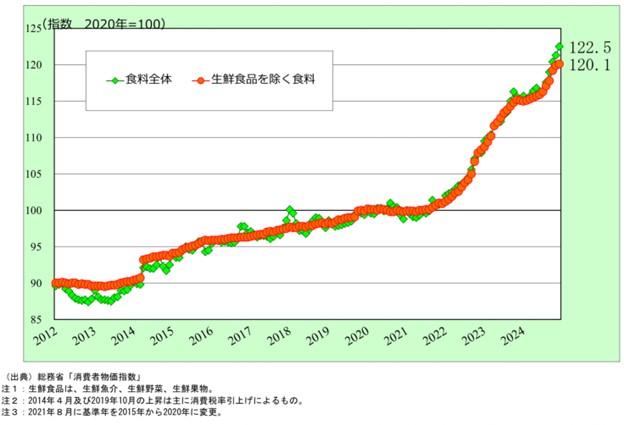
図2　食料の消費者物価指数の推移（全国：2012年１月～2024年12月）

2020年の物価指数を100とすると、2024年12月には食料全体で122.5にまで上昇しています。

生きるのに必要な食料品は節約することが難しいため、こうした状況では食料品への支出が増加し、結果としてエンゲル係数が上昇していると指摘されています。*2

エンゲル係数の変化には高齢化の進展や世帯数の増加、生活スタイルの変化なども影響するため、その解釈は慎重に行う必要があります。

しかし、生きていく上で欠かせない食料への支出割合が大幅に上昇していることによって、生活にゆとりを感じにくい状況になっていることは間違いないでしょう。

一人暮らしのエンゲル係数

一人暮らしのエンゲル係数は実際にはどの程度なのでしょうか。
また、食料費の目安はどのくらいでしょうか。

2024年のエンゲル係数

単身世帯のエンゲル係数を算出してみましょう。
2024年の家計調査の区分「単身世帯・勤労者世帯　男女, 年齢階級別」から34歳以下の男女平均のデータをみると、消費支出が176,160円、食料費が40,305円となっています。*6
これをエンゲル係数の数式に当てはめると、以下のようになります。

　40,305円（食料費）÷ 176,160円（消費支出）× 100 ≒ 22.9

上述のように、2024年の二人以上世帯のエンゲル係数は27.1％でしたから、それを下回っています。

ただし、男性だけに絞ると、異なる状況がみえてきます。
家計調査の同区分で男性をみると、消費支出が147,708円、食料費が40,308円となっています。*6
これをエンゲル係数の数式に当てはめると、以下のようになります。

　40,308円（食料費）÷ 147,708円（消費支出）× 100 ≒ 27.3

したがって、一人暮らしの男性のエンゲル係数は二人以上世帯のエンゲル係数と同程度ということになるのです。

食料費の目安

食料費の目安は給与の手取りの15％程度にすることが推奨されています。*7
また、手取りは一般的には額面のおよそ75～85％といわれています。*8
この割合を当てはめて給与の手取り額とその15％に当たる金額を求めたのが以下の表1です。

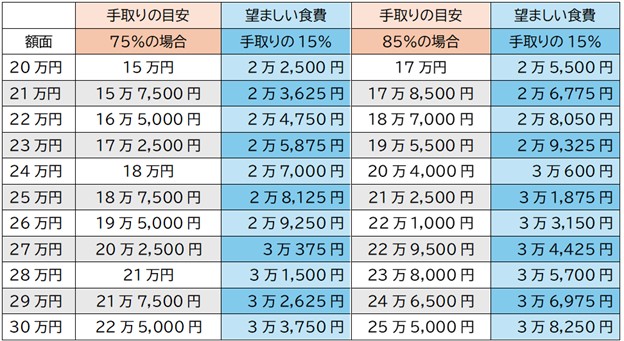
表1　「手取・望ましい食料費の目安」

先ほどみたとおり2024年の34歳以下の食料費（男女平均）は40,305円ですから、額面30万円の食料費の目安を上回っていることになります。

食料費の節約法と貯蓄術

では、食料費はどのようにしたら節約できるのでしょうか。
また賢く貯蓄するためにはどうしたらいいのでしょうか。

食料費の節約法

2024年の家計調査の数値をみると、節約できそうな項目があります。
34歳以下の単身世帯の食料費で最も大きな割合を占めるのは外食の17,533円で、食料費全体の約43.5％を占めています。*6

ちなみに、家計調査のうち総世帯平均（世帯人数2.17人）をみると食料費は69,530円で、そのうち外食の支出は12,423円、食料費全体の約17.9％に相当します。
したがって、34歳以下の単身世帯の外食費は世帯人数2.17人の総世帯平均を5,110円も上回っていることになるのです。*9

そう考えると、週に何回かはランチを持参するなどして外食を少し控えるだけでも節約効果があるかもしれません。
毎月、食料費として手取りの15％を割り振り、その範囲内におさまるように工夫してみてはいかがでしょうか。

また、買った食品を無駄にせず、使い切り食べ切ることも大切です。
日本では本来食べられるにもかかわらず捨てられている食品、「食品ロス」が年間472万トン、国民1人当たりの経済損失として計算すると年間約32,000円に上ります。*10
その半分が各家庭から発生する食品ロスです。

家庭からの食品ロスは主に食べ残したり、手つかずの食品をそのまま捨ててしまったり、皮を剥きすぎたりすることなどが原因です。

食品ロスを防ぐためには、買物をする際に「買いすぎない」こと、料理を作る際に「作りすぎない」こと、そして「食べきる」ことが大切です。

一人暮らしの貯蓄術

食料費の節約法を考えたところで、貯蓄術も考えてみましょう。

貯蓄にお金を回すためには、無駄遣いをなくす必要があります。*11
まずは1か月間、自分が使ったお金をスマホやメモに記録します。
クレジットカード払いの分はカード明細をチェックします。
そうしたお金の管理には「家計簿アプリ」を活用すると便利です。

手間をかけずに出費を抑えるためには、毎月きまってかかる固定費や無駄遣いにつながる習慣を見直すことが早道です。

下の見直しチェックシートを活用してみましょう。

図3　「支出見直しチェックシート」

支出を見直したら、先に貯蓄をし、余った分で生活します。
たとえば給与振り込み口座がある銀行で積み立て用の口座を開けば、別口座に振り込む手間をかけなくても、毎月決まった日に自動的に定額が積立定期預金に振り替えられ、貯まっていきます。

運用で得た利益を元本にプラスして再投資し、その合計金額をもとに利益を得る「複利」にすれば、運用期間が長くなるほど発生する利益の金額が大きくなります。*12
こうした「複利効果」もあるため、始めるのが早いほど無理なく貯めることができます（図4）。

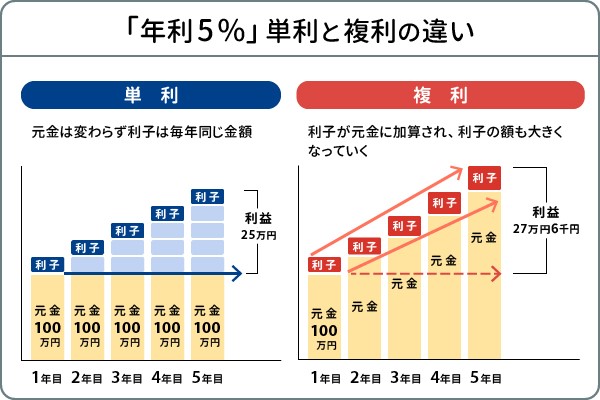
図4　「複利効果」

おわりに

食料費は手取りの15％程度という目安がありますが、一人暮らしの外食費は総世帯の平均より多く、そこに節約のヒントがありそうです。

食料費を見直して節約できたら、それを機に家計簿アプリなどを上手に活用して家計管理をし、賢く貯蓄しましょう。
自動積立定期預金などを利用すれば、無理なく貯蓄を継続できます。

節約と貯蓄を習慣化し、理想のライフスタイルを実現しましょう。

本コラム執筆時点における情報に基づいて作成しておりますので、最新情報との乖離にご注意ください。
最終的な投資判断、金融商品のご選択に際しては、お客さまご自身の判断でお取り組みをお願いいたします。

出典
*1 総務省統計局「家計調査　用語の解説」
*2 第一生命経済研究所「【1分解説】エンゲル係数とは？」（2025年1月17日）
*3 金融広報中央委員会 知るぽると「エンゲル係数とは」
*4 第一生命経済研究所「Economic Trends　テーマ：エンゲル係数上昇の主因は家計の節約 ～実質可処分所得増加による押し下げを消費性向低下による押し上げが上回る～ 」（2025年2月10日）p.1, 2
*5 農林水産省「食料の消費者物価指数の推移」p.1
*6 e-Stat「統計で見る日本　家計調査2024年＞単身世帯・勤労者世帯　男女，年齢階級別」から「EXCEL閲覧用 第2表」
*7 東京証券取引所　東証マネ部！「今日からすぐに実践！無理せずできる7つの食費節約テクニック」（2020年7月23日）
*8 三菱ＵＦＪニコス「手取り計算の方法は？月収・年収の額からわかる早見も紹介」（2025年3月3日）
*9 e-Stat「統計で見る日本　家計調査2024年＞家計調査 家計収支編 総世帯」
*10 政府広報オンライン「食品ロスを減らそう！今日からできる家庭での取組」（2025年1月17日）
*11 日本FP協会「若手社会人のマネー＆ライフプラン＞CHAPTER2・対策編　お金の不安を解消するために行動しよう」（2023年1月改訂・2023年12月追補）p.18, 19, 20
*12 三菱ＵＦＪ銀行「複利とは？複利の効果や計算式、有効な活用法をわかりやすく解説」